Please go to update pages for the latest modification, class-wise issues, and others if links for those pages exist.
update page a  update page b   update page c

Lab work modification: TBD (after class survey and Lab 4)

Objectives and Outcomes:

• Learn about the capacitor and its basic circuit behaviors
• Build and watch demonstration circuits that illustrate:
  
• Capacitor charge and discharge behavior vs circuit resistance
  
• Capacitor in R C (resistance and capacitance) circuit that illustrates relationship between RC time and frequency
  
• Capacitance for differentiation & high-pass filter, and integration & low-pass filter.
  

Overview:

Part Introduction  Review (from lecture courses) of capacitor basic properties

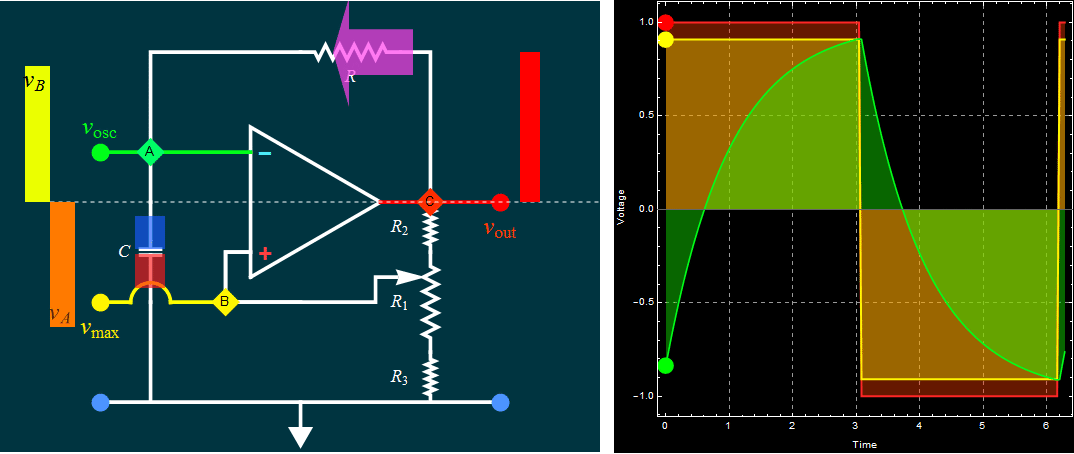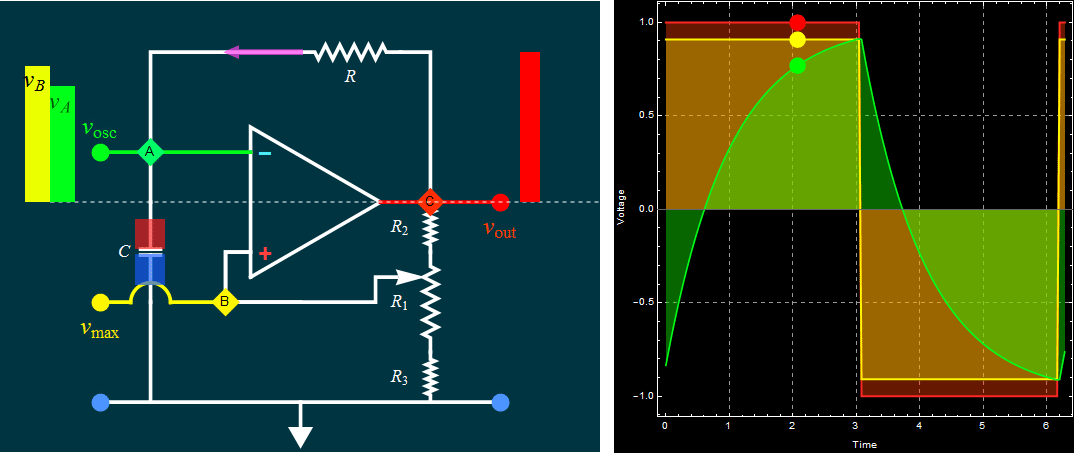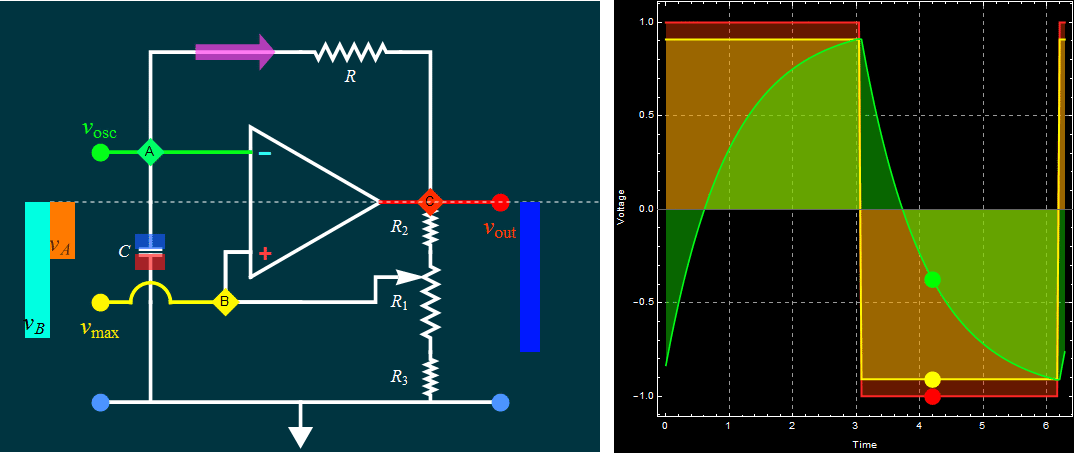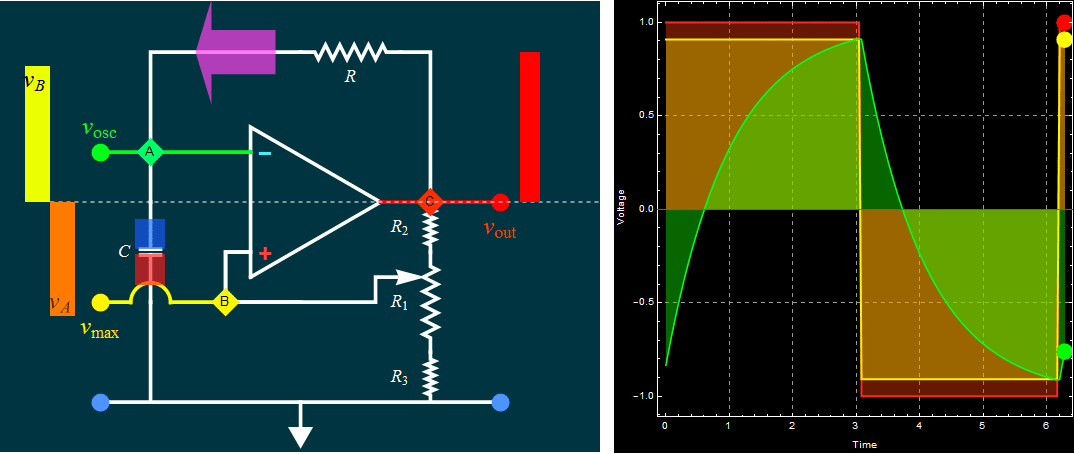
Part A:  Op amp self-oscillation circuit: RC time in charge, discharge, and oscillation frequency

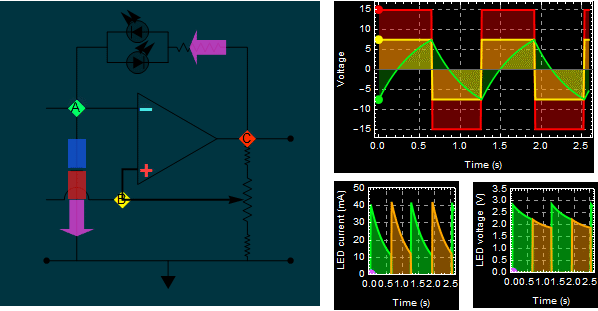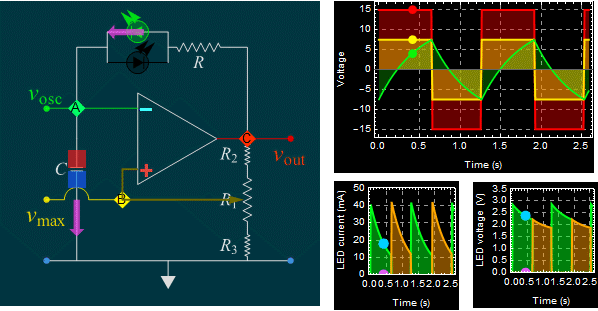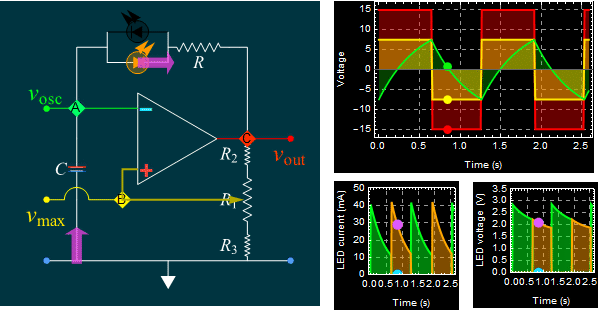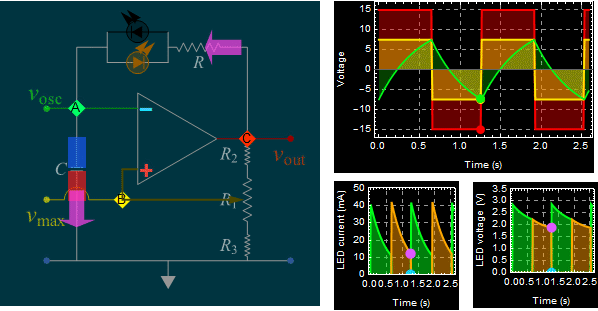Part B       Differentiation circuit and high pass behavior

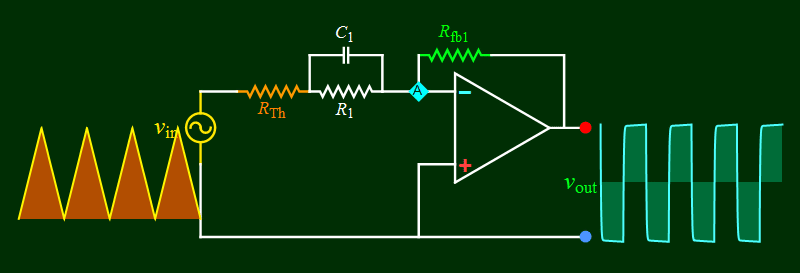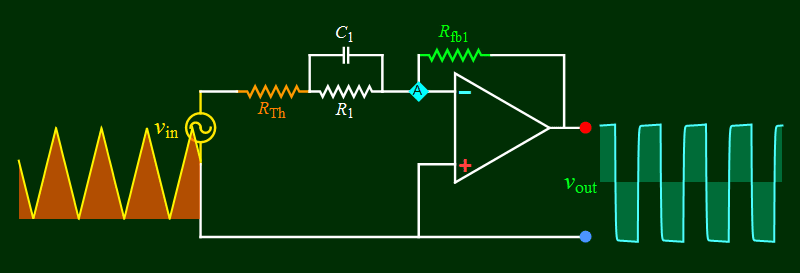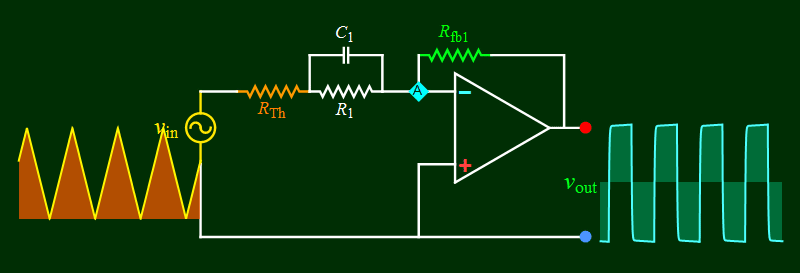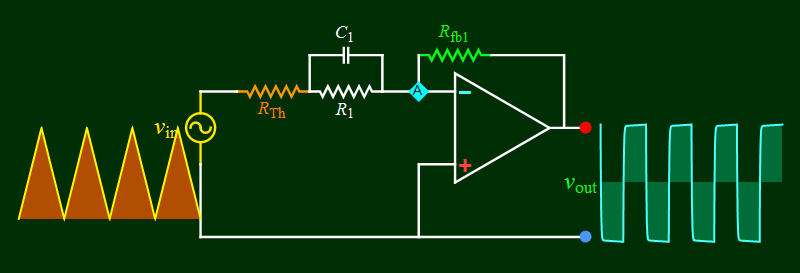Part C        Integration circuit and low-pass behavior

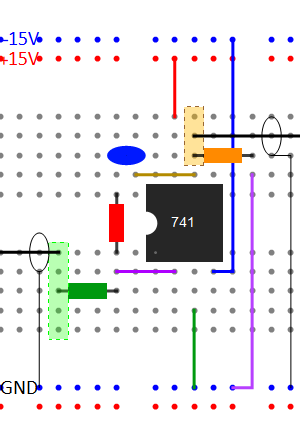
Lab work


Part 0: Introduction

Step 1: If electrons from a source are blocked from making a round trdip of a circuit, or are not even allowed to enter into circuit elements, can the source supply power to the circuit elements? Can the circuit work?




 
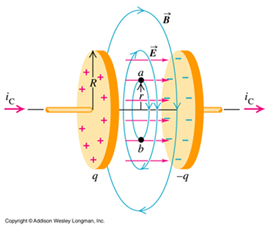
Step 2: When a voltage V is applied to a capacitor, the capacity stores a charge q=C*V, where C is its capacitance. Can this charged capacitor give a current to a circuit, and what is the relationship of its voltage v[t], charge  q[t] (t is time) and its current?

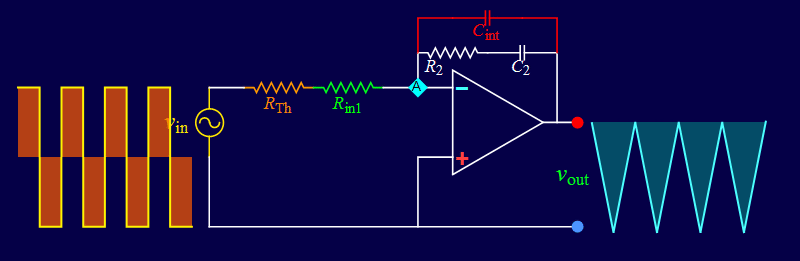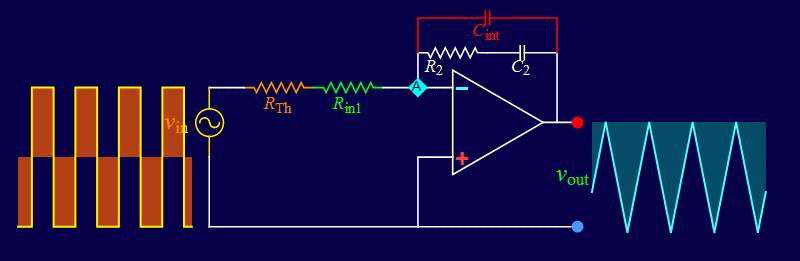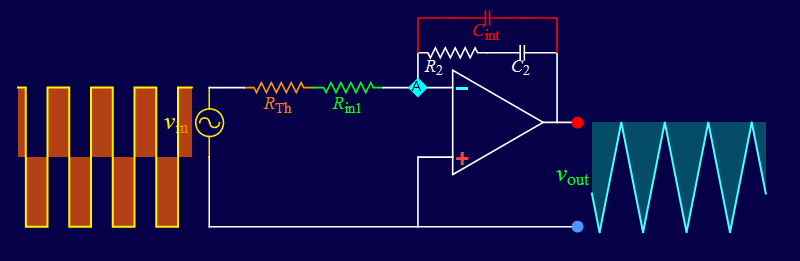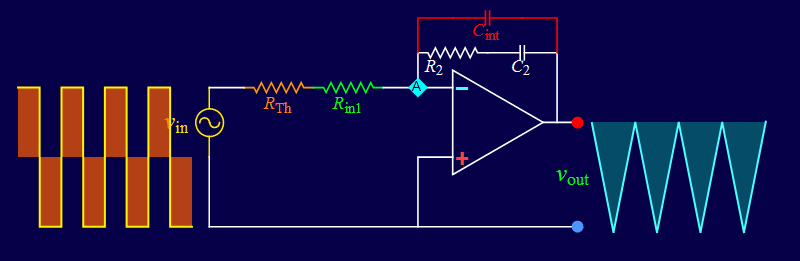
Step 3: Based on the op amp negative-feedback usage, an input current, such as that of a capacitor, can be converted to a voltage with a feedback resistance. Is it possible to use an op amp to give a voltage output proportional to the time-derivative of an input voltage?


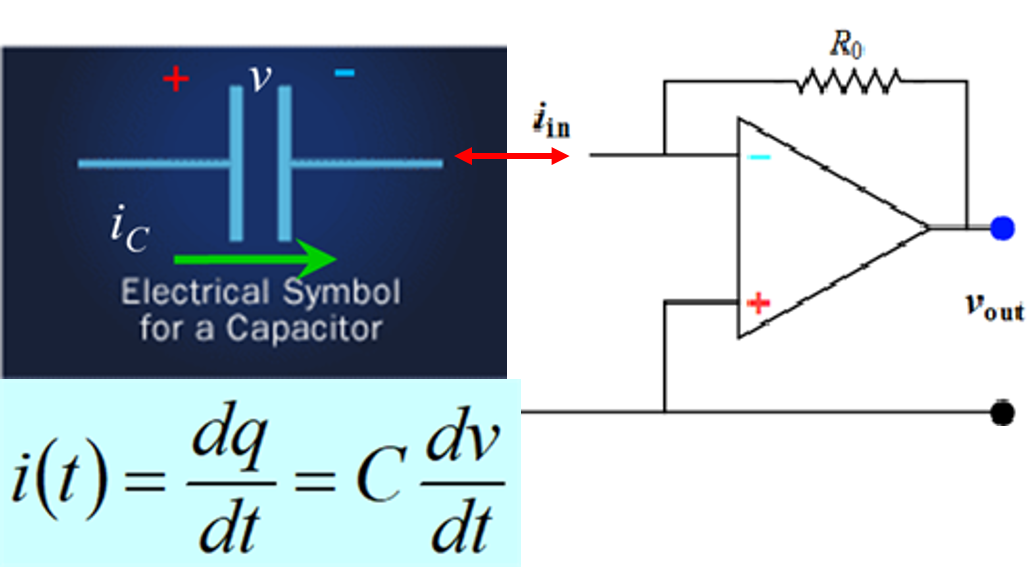
Step 4: Given the relationship between a capacitor voltage and its current as given previously:


If the capacitor voltage is known, taking its time derivative will give the current. If the current is known, is it possible to obtain the voltage? How?



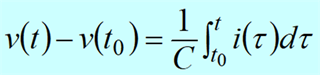
Step 5: Based on the op amp negative-feedback usage, given an input current, a feedback capacitor will integrate the current. Is it possible to use an op amp to give a voltage output proportional to the integral of an input voltage?

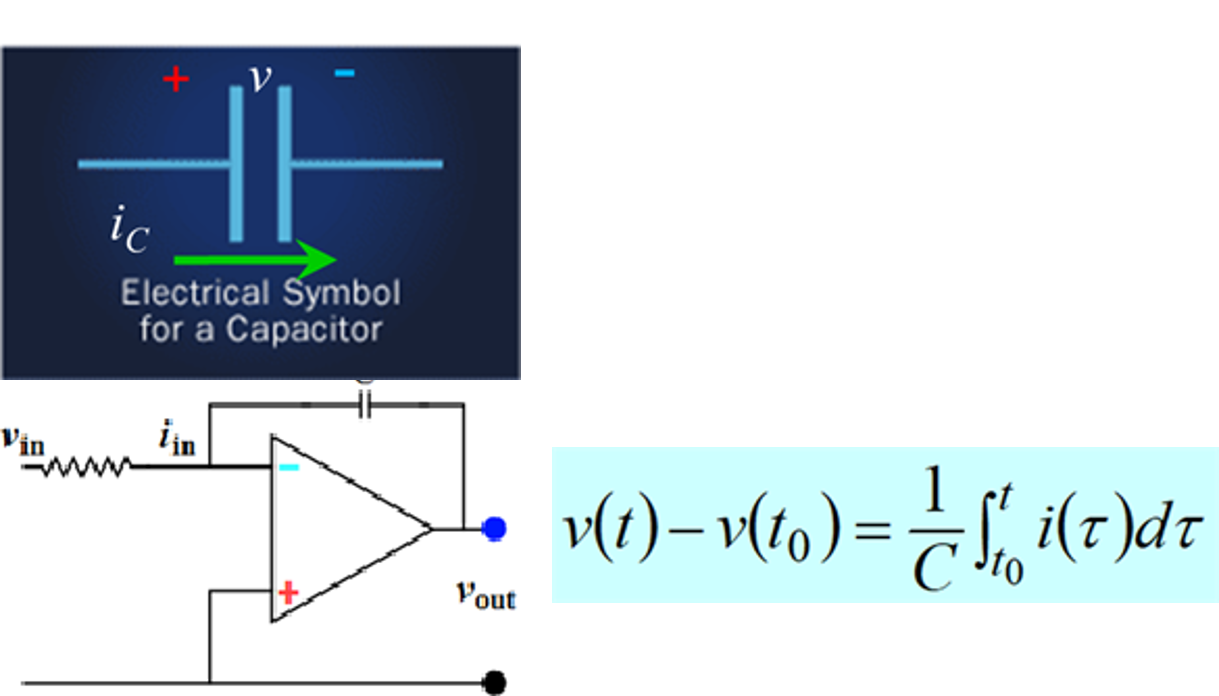
This configuration is also very popularly known as capacitive transimpedance amplifier that is ubiquitous in the readout circuit of every cell phone camera, or virtually all CMOS cameras for that matter as shown in the reference below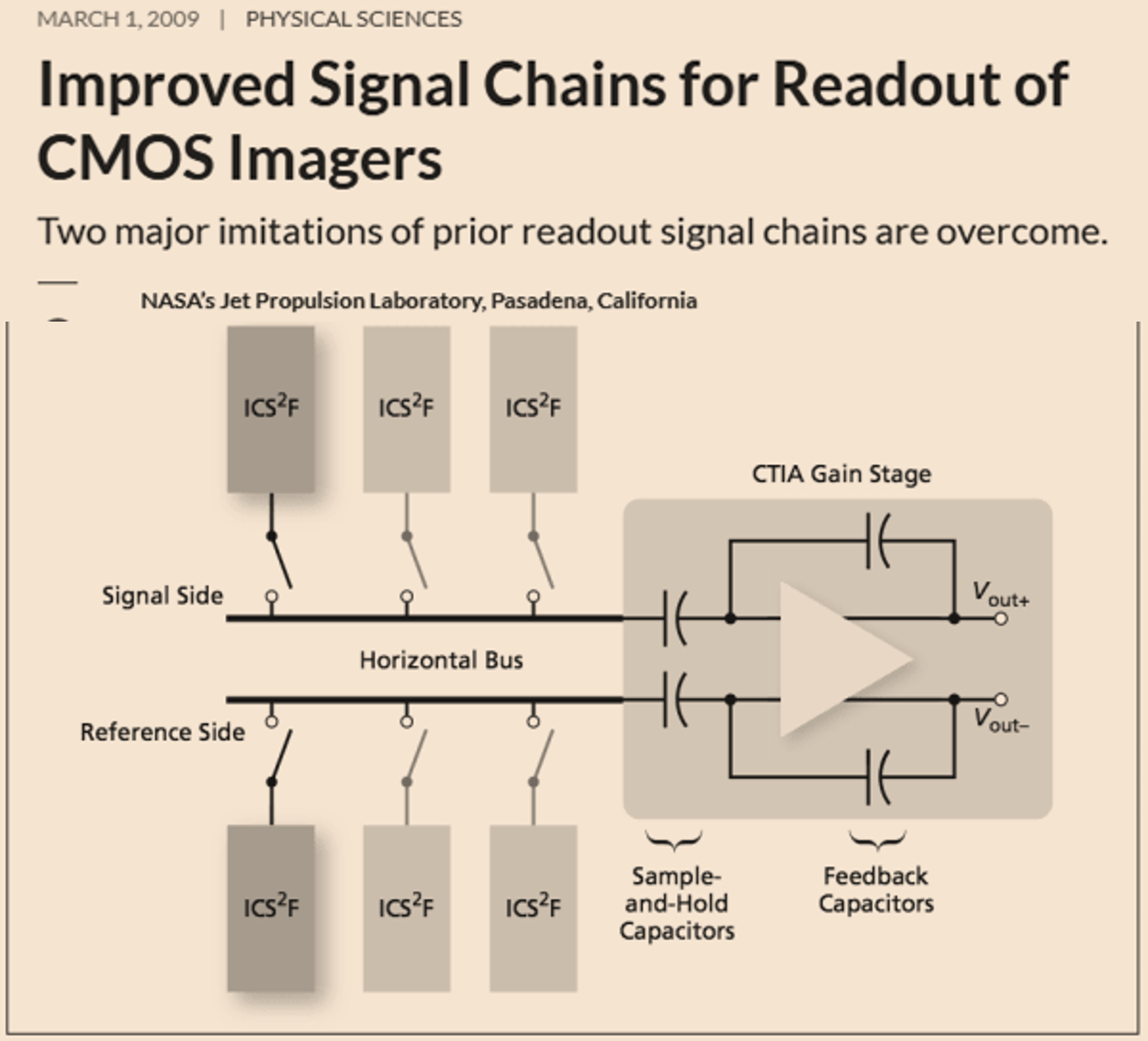

End of Part 0: Introduction



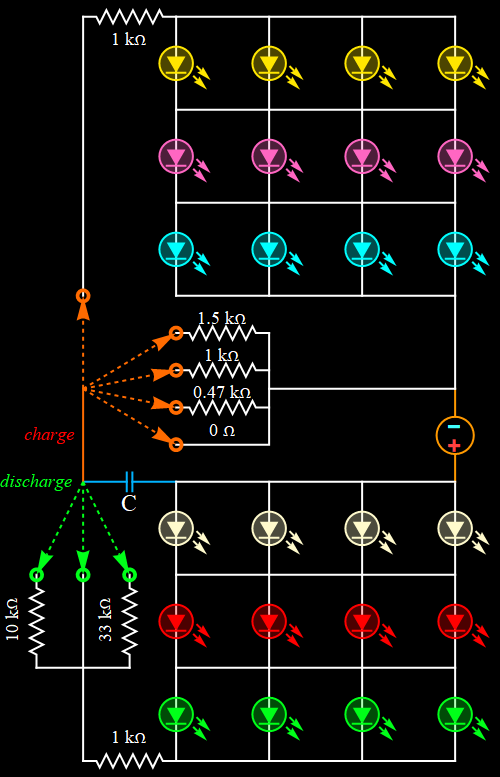
Part A: Capacitor charge and discharge behavior


Step 1: Observe the demonstration of capacitor charging behavior. Interpret and report.

Experiment 1: how fast can a capacitor be charged?

 


 

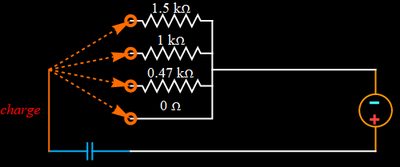
Example of actual circuit for experiment:






 

Experiment 2: discharging behavior: how fast can a capacitor discharge?

 



Experiment 3: The symmetry of current behavior in charging and discharging.






For capacitor, capacitance matters. Comparison of 470-uF capacitor to a 10-uF one:











End of Part A - Step 1

 
Continue to page 2